Research
DINUMA
Project funded EU FP7 Program, Marie Curie International Incoming Fellowship (PIIF-GA-2010-275823)
Project Overview
To improve diagnosis, monitoring and treatment of traumatic brain injury (TBI) and normal pressure hydrocephalus (NPH), there is a need to understand the fundamental mechanical processes underlying the disease progression. The development of multi-scale simulation-based environments for biomedical applications is an emerging field, which holds great promises as a tool to explore in vivo fluid and structural mechanics to a level of details not achievable experimentally and under any desired conditions. Through this detailed understanding, we aim to define better monitoring and control strategies for NPH and TBI patients, thereby transferring our knowledge to the clinical and patient community. This model will address the key shortcomings of the current strategies, namely the lack of integration between structural and fluid components and the discrepancies between the parenchymal deformations under large or small strain rates
Motivation
Brain-related diseases are a major cause of death and disability worldwide. Traumatic brain injuries (TBI) – due to falls, violence, vehicle accidents – account for 1 million hospital admissions per year and an annual cost of €10-20 billion in the European Union alone). The cost of dementia was estimated to an additional €55 billion, including patients suffering from Alzheimer’s disease, Parkinson’s disease, but also misdiagnosed patients suffering from normal pressure hydrocephalus (NPH). Lack of specialized tools and protocols targeted to the different neurological disorders leads to diagnosis errors and/or inadequate treatment strategies, resulting in financial and societal costs which could be otherwise avoided. As an example, intracranial pressure (ICP) monitoring to detect cerebral hemorrhage in TBI patients has certainly reduced mortality rates, but whether or not intracranial pressure will rise above a set threshold is difficult to anticipate, and the ICP rise often occurs too suddenly for the intensive care unit staff to prepare the appropriate intervention. Another example is the diagnosis of NPH, which is a reoccurring problem faced by clinicians due to the overlap of symptoms and diagnostic findings between NPH and other neurodegenerative pathologies such as Alzheimer’s disease. Statements exemplified by “the causes and pathophysiology of idiopathic NPH still remain poorly understood” are commonly found in literature on NPH, highlighting a lack of fundamental understanding of the disease mechanism, which in turn translates into sub-optimal or even erroneous treatment choices. Such scenario is not specific to NPH or TBI, and treatment limitations due to a lack of understanding of the intra-cranial mechanics may be found throughout the spectrum of neurologic disorders. A major difficulty is that the large number of variables (inter-patient variability, inter-institution variability) and possible pathways (biochemical, electrical, mechanical), and difficulty to acquire detailed measurements within the brain make it challenging to resolve disease mechanisms based on clinical data alone. This is the typical setting where numerical modeling tools could make a significant impact by providing a controlled hypothesis test-bed, ultimately allowing researchers to identify the most probable disease mechanism and later develop adequate diagnosis and treatment protocols.
Brain Structure and Mechanical Behavior
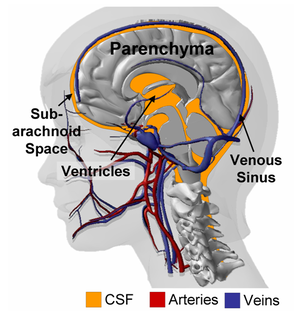
As illustrated in Figure 1, the intra-cranial space contains the parenchyma (i.e. white and gray matters) suspended in cerebrospinal fluid (CSF) and perfused by a multitude of veins, arteries and capillaries. The brain parenchyma consists of a dense network of neuronal cell bodies and interconnecting fibers filled with interstitial fluid. Miller et al. showed that, under moderate strain rates, the parenchyma could be approximated as an incompressible non-linear visco-elastic material. However, such description fails to explain the deformations observed under quasi-static load (such as those happening during convolutional development or during hydrocephalus, for example). Franceschini et al. demonstrated that under unconfined, quasi-static compression, the human brain behaves follows the consolidation theory for fine soils, where the intra-cerebral fluid is progressively squeezed out of the parenchyma. In addition to the recent evidences provided by Franceschini and coworkers, there are number of instances pointing to the fact that the porous, bi-phasic nature of the brain should not be ignored; starting with the nature of cerebral edema itself, or the volumetric shrinking of the brain observed after hyperosmotic drugs administration (such as mannitol). The series of data presented by Hakim and co-workers also emphasize the role played by the interstitial cerebral fluid on the parenchymal deformations during hydrocephalus. All of these results combined, suggest that the brain tissue should be modeled as a porous, fluid-saturated material, with a non-linear visco-elastic solid phase and exhibiting a very small volumetric compressibility.
Numerical Modeling Strategy
The objective of this study is to devise a novel porous formulation for the brain parenchyma that reconciles the different mechanical behaviors reported in literature depending on the loading conditions. To this end we developed a multi-scale bottom-up model of the brain, wherein we explicitly model the subscale mechanics to obtain macro-scale cerebral behavior. The brain’s structure is classified into meso- and macro-scale domains. The mesoscale considers the anisotropic organization of fiber tracts and differentiates between blood and ISF, while the macroscale differentiates between brain tissue, larger blood vessels and CSF. Macro-scale brain tissue properties are obtained from the mesoscale by homogenization. Accordingly, the macro-scale behavior depends on macro-scale loading conditions such as changes in ventricular volume and on the mesoscale properties.
If one assumed porous material properties to remain constant throughout the deformation, our formulation would reduce to the consolidation theory of Biot. However, while assuming constant properties is often valid in soil mechanics, it does not hold for brain mechanics where deformations can be large. In contrast, our multi-scale formulation allows for the dynamic adjustment of the local material properties: Deformations at the macroscale impact the mesoscale structure, which in turn affects the average mesoscale properties. In addition, Biot’s theory requires fitting of model parameters such as porosity to experimental data, whereas in our approach these parameters are obtained from the computations at the mesoscale.
This multi-scale framework is implemented within the open-source platform OpenFOAM. It uses a finite volume formulation that can handle meso- and macroscale problems of any geometric configuration, using either structured or unstructured grids. Since resolving the mesoscale problems at each iteration is computationally expensive, we pre-compute the different mesoscale configurations and store the results in a look-up table.
Preliminary Results
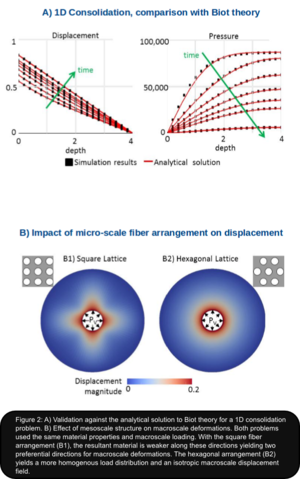
Preliminary results are presented in Figure 2: Panel A shows excellent agreement in the validation of our computational framework against the analytical solution of an equivalent Biot problem. Panel B exemplifies the impact of two different mesoscale configurations in a simplified 2D axisymetric problem. The macroscale geometry is subjected to homogenous pressure loading from the inside, representing increased ventricular pressure. Zero displacement conditions are applied at the outside wall to reflecting the rigidity of the adult skull. The mesoscale domain encompasses one solid phase to account for fiber tracts and one fluid phase representing lumped blood and ISF. The fluid is Newtonian and the fibers are modeled as isotropic linear elastic. Despite the isotropic mesoscale material formulation, anisotropic macro-scale behavior arises from the anisotropic fiber arrangement. In the rectangular fiber arrangement (Figure. 2, B1), the fluid cavities are aligned along the vertical and horizontal axes. The resultant material is weaker along these directions yielding two preferential directions for the macro-scale deformation. In contrast, the hexagonal arrangement (Figure. 2, B2) leads to a more homogenous load distribution and an isotropic macro-scale displacement field.